Problem Statement
The NeoCubist artistic movement has a very distinctive approach to art. It starts with a rectangle which is divided into a number of squares. Then multiple rounds of layering and scraping occur. In a layering round, a rectangular region of this canvas is selected and a layer of cubes, 1 cube deep, is added to the region. In a scraping round, a rectangular region of the canvas is selected, and a layer of cubes, again 1 cube deep, is removed.
The famous artist I.M. Blockhead seeks your help during the creation of this artwork. As he is creating his art, he is curious to know how many blocks are in different regions of the canvas.
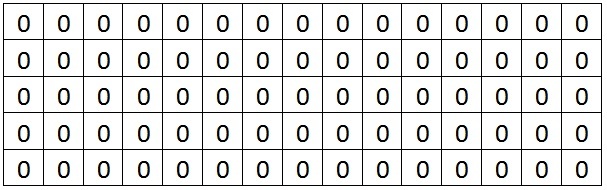
Your task is to write a program that tracks the creation of a work of Pseudo-Cubist art, and answers I.M.’s periodic queries about the number of blocks that are on the canvas. Consider, for example, the following artwork created on a canvas with 5 rows and 15 columns or squares. The canvas starts without any blocks, like in the figure below. We label cells in the canvas based on the tuple (row,column), with the upper left corner being designated (1,1). The numbers in each cell represent the height of the blocks in that cell.
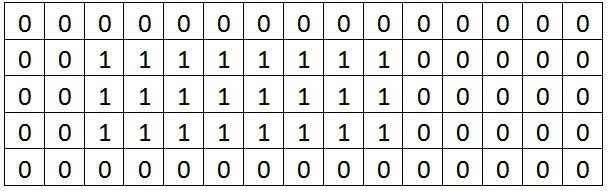
After adding a layer in blocks to the rectangle with upper left corner at (2,3) and a lower right corner of (4, 10), the canvas now looks like the following:
After adding a layer of blocks in the rectangle with upper left corner at (3,8) and a lower right corner of (5, 15), the canvas now looks like the following:
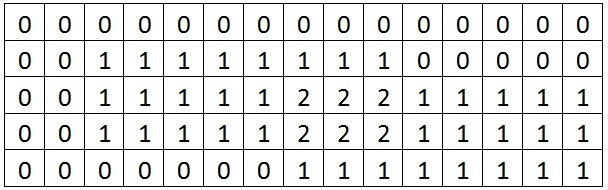
If Blockhead were to ask how many blocks are currently in the artwork in the rectangle with upper left corner (1,1) and lower right corner (5,15), you would tell him 48.
Now, if we remove a layer of blocks from the rectangle with upper left corner at (3,6) and a lower right corner of (4, 12), the canvas now looks like the following:
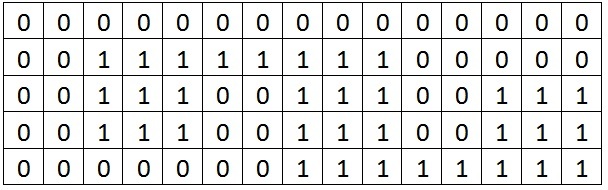
If Blockhead were to ask how many blocks are now in the artwork in the rectangle with upper left corner (3,5) and lower right corner (4,13), you would tell him 10.
“Beautiful!” exclaims Blockhead.
Input Format
The first line in each test case are two integers r and c, 1 <= r <= 12, 1 <= c <= 106, where r is the number of rows and c is the number of columns in the canvas.
The next line of input contains an integer n, 1 <= n <= 104.
The following n lines of input contain operations and queries done on the initially empty canvas. The operations will be in the following format:
[operation] [top left row] [top left column] [bottom right row] [bottom right column]
[operation] is a character, either “a” when a layer of blocks is being added, “r” when a layer of blocks is being removed, and “q” when Blockhead is asking you for the number of blocks in a region.
The remaining values on the line correspond to the top left and bottom right corners of the rectangle.
Note: You will never be asked to remove a block from a cell that has no blocks in it.
Output Format
For each “q” operation in the input, you should output, on a line by itself, the number of blocks in the region of interest.
Sample Input
5 15 5 a 2 3 4 10 a 3 8 5 15 q 1 1 5 15 r 3 6 4 12 q 3 5 4 13
Sample Output
48 10
My Solution 🙂
import java.util.*;
public class BlockArt {
public static void main(String[] args) {
// TODO Auto-generated method stub
Dim query = null;
int r, c, op, ulr, ulc, brr, brc, interestVal = 0;
String operation;
Scanner sc = new Scanner(System.in);
r = sc.nextInt();
c = sc.nextInt();
op = sc.nextInt();
int[][] canvas = new int[r + 1][c + 1];
ArrayList<Dim> list = new ArrayList<>();
for (int i = 0; i < op; i++) {
operation = sc.next();
ulr = sc.nextInt();
ulc = sc.nextInt();
brr = sc.nextInt();
brc = sc.nextInt();
if(operation.equals("a")) {
list.add(new Dim('a', ulr, ulc, brr+1, brc+1));
}
if (operation.equals("r")) {
list.add(new Dim('r', ulr, ulc, brr+1, brc+1));
}
if(operation.equals("q")) {
query = new Dim(ulr, ulc, brr+1, brc+1);
for (Dim obj : list) {
switch(obj.op){
case 'a':
interestVal = interestVal + intersectionCount(obj, query);
break;
case 'r':
interestVal = interestVal - intersectionCount(obj, query);
break;
}
}
System.out.println(interestVal);
interestVal = 0;
}
}
}
public static int intersectionCount(Dim d, Dim q){
return Math.max(0, Math.min(d.x2, q.x2) - Math.max(d.x1, q.x1)) *
Math.max(0, Math.min(d.y2, q.y2) - Math.max(d.y1, q.y1));
}
public static class Dim{
public char op;
public int x1;
public int y1;
public int x2;
public int y2;
public Dim(char c, int x1, int y1, int x2, int y2) {
this.op = c;
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
public Dim(int x1, int y1, int x2, int y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
}
}
~Rajind Ruparathna